Last update=23 May, 2006

There are 51 connected vertex-transitive graphs on 14 vertices. There are 3 of degree 3 (21 edges), and 5 of degree 4 (28 edges). These are shown here. The order of the automorphism group is given in square brackets in each window's title.

Notation:

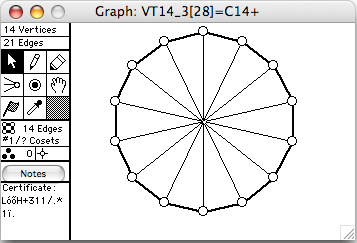
• C_n means the cycle of length n
• C_n⁺ means the cycle of length n with diagonals
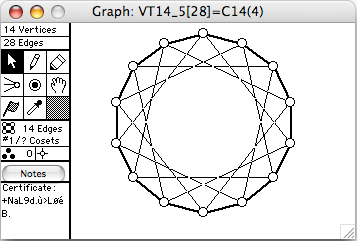
• C_n(k)  means the cycle of length n with chords of length k
• C_n(k⁺)  means the cycle of length n with chords of length k from every second vertex
• ~G   means the complement of G
• 2G   means two disjoint copies of G
• GxH   means the direct product of G and H
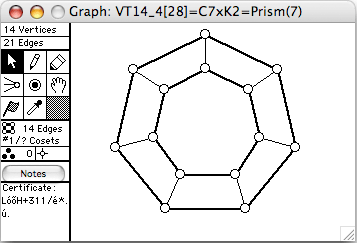
• Prism(m)  means C_mxK₂, ie, two cycles with corresponding vertices joined by a matching
• BiDbl(G)   means the bipartite double of G. Make 2 copies of V(G), call them u₁,...,u_n and v₁,...,v_n. If uv is an edge of G, then u₁v₂ and v₁u₂ are edges of BiDbl(G)
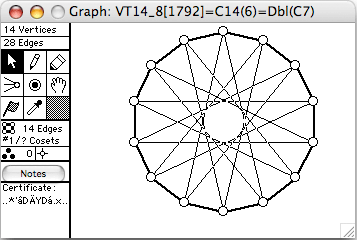
• Dbl(G)   means the double of G. Make 2 copies of G, call them G₁ and G₂. If uv is an edge of G, then u₁v₂ and v₁u₂ are also edges of Dbl(G)
• Dbl⁺(G)   means the double of G, with the additional edges u₁u₂
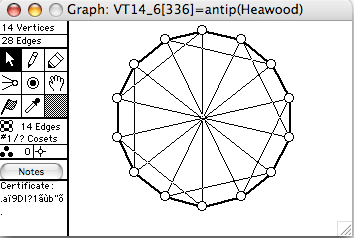
• antip(G)  means the antipodal graph of G. It has the same vertices, but u and v are joined in antip(G) if they are are maximum distance in G

The complements of the graphs shown here and the complements of the disconnected transitive graphs are:

VT12_39 = ~C₁₄(4)

VT12_40 = ~2C₇(2)

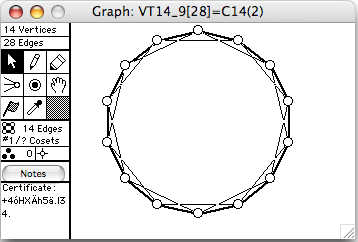
VT12_41 = ~C₁₄(2)

VT12_42 = ~C₁₄(6)=~Dbl(C₇)

VT12_43 = ~antip(Heawood)

VT12_44 = ~C₁₄(3)=~BiDbl(C₇(2))

VT12_45 = ~(C₇xK₂)=~Prism(7)

VT12_46 = ~C₁₄⁺

VT12_47 = ~Heawood

VT12_48 = ~2C₇

VT12_49 = ~C₁₄

VT12_50 = ~7K₂

VT12_51 = ~K₇

The Heawood graph is the incidence graph of the Fano plane, the unique projective plane with 7 points and 7 lines. The Heawood graph is also known as the (3,6)-cage. It is also the dual of the unique embedding of K₇ on the torus, which is basically how Heawood discovered it.

    Back to the Groups & Graphs home page.