Last update=23 May, 2006

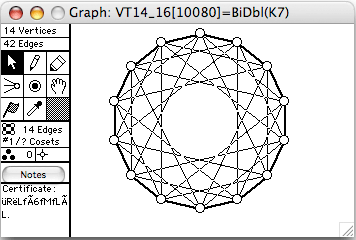
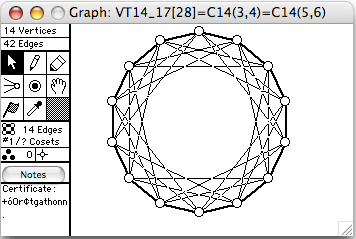
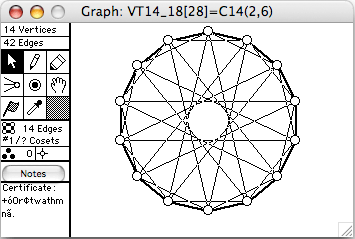
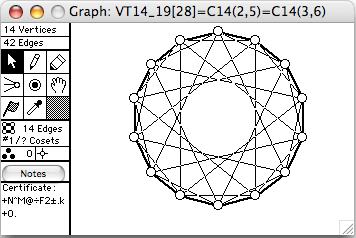
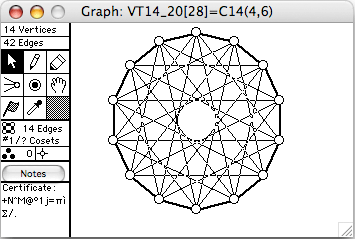
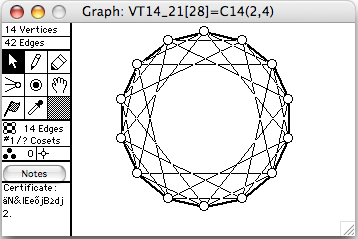
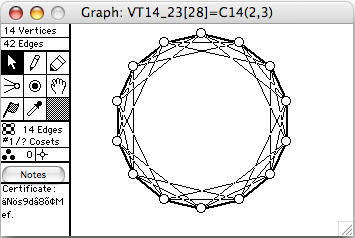
There are 51 connected vertex-transitive graphs on 14 vertices. The 8 of degree 6 (hence 42 edges) are shown here. The order of the automorphism group is given in square brackets in each window's title.

Notation:

• C_n means the cycle of length n
• C_n⁺ means the cycle of length n with diagonals
• C_n(k)  means the cycle of length n with chords of length k
• C_n(k⁺)  means the cycle of length n with chords of length k from every second vertex
• ~G   means the complement of G
• 2G   means two disjoint copies of G
• GxH   means the direct product of G and H
• Prism(m)  means C_mxK₂, ie, two cycles with corresponding vertices joined by a matching
• L(G)   means the line-graph of G
• BiDbl(G)   means the bipartite double of G. Make 2 copies of V(G), call them u₁,...,u_n and v₁,...,v_n. If uv is an edge of G, then u₁v₂ and v₁u₂ are edges of BiDbl(G)
• Dbl(G)   means the double of G. Make 2 copies of G, call them G₁ and G₂. If uv is an edge of G, then u₁v₂ and v₁u₂ are also edges of Dbl(G)
• Dbl⁺(G)   means the double of G, with the additional edges u₁u₂

The complements of the graphs shown here are:

VT12_24 = C₁₄⁺(3,5)=~2K₇

VT12_25 = ~C₁₄⁺(4,3⁺)

VT12_26 = C₁₄⁺(2,4)=~C₁₄(2,3)

VT12_27 = C₁₄⁺(2,5)=~C₁₄(2,6)

VT12_28 = C₁₄⁺(4,6)=~C₁₄(3,4)

VT12_29 = C₁₄⁺(3,4)=~C₁₄(4,6)

VT12_30 = C₁₄⁺(2,3)=~C₁₄(2,4)

VT12_31 = C₁₄⁺(2,6)=~C₁₄(3,6)

VT12_32 = K₇xK₂=~BiDbl(K₇)

    Back to the Groups & Graphs home page.